En este artículo exploraremos el fascinante mundo de las curvas concavas y convexas. Descubriremos cómo estas curvas juegan un papel crucial en diversas disciplinas, desde la matemática hasta el diseño de productos. Acompáñanos en este viaje para comprender mejor la belleza y la importancia de las curvas en nuestro entorno. ¡No te lo pierdas!
¿Cuando una curva es cóncava o convexa?
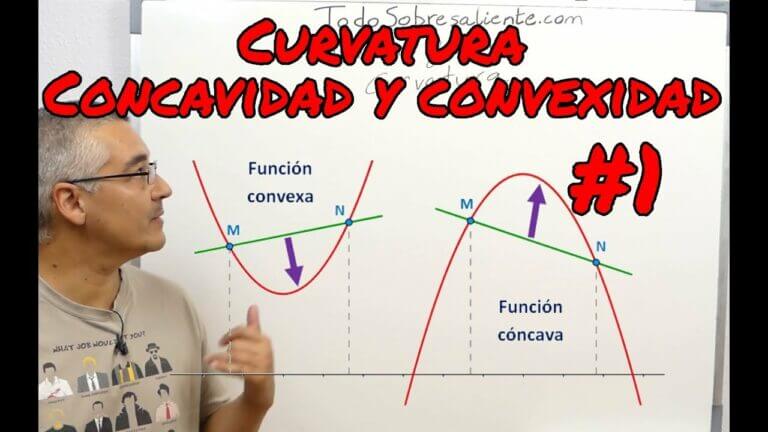
La concavidad de una curva se determina por la forma en que la gráfica de la función se posiciona en relación a las rectas tangentes alrededor de un punto. Si la gráfica queda por debajo de las rectas tangentes, se dice que la curva es cóncava hacia abajo, y en este caso también se puede decir que es convexa.
¿Cuándo se sabe si es cóncava o convexa?
Para determinar si una función es cóncava o convexa, se puede observar cómo se relaciona la gráfica de la función con la recta tangente en cada punto. Si la gráfica queda por debajo de la recta tangente en todos los puntos, entonces la función es cóncava. Por otro lado, si la gráfica queda por encima de la recta tangente en todos los puntos, la función es convexa.
Un criterio importante para determinar la concavidad o convexidad de una función es el criterio de la segunda derivada. Si la segunda derivada de la función es negativa (f ” 0), entonces la función es cóncava.
En resumen, para identificar si una función es cóncava o convexa, se puede analizar la relación entre la gráfica de la función y la recta tangente en cada punto, así como aplicar el criterio de la segunda derivada. Si la función queda por debajo de la recta tangente y la segunda derivada es positiva, la función es cóncava; si queda por encima de la recta tangente y la segunda derivada es negativa, la función es convexa.
¿Cuál es la diferencia entre cóncavo y convexo?
La diferencia entre cóncavo y convexo radica en la medida de los ángulos interiores de un polígono. Los polígonos convexos son aquellos en los que todos sus ángulos interiores miden menos de 180 grados. Por otro lado, los polígonos cóncavos se caracterizan por tener uno o más ángulos interiores que miden más de 180 grados.
Los polígonos convexos son comunes en la geometría, ya que todos los polígonos regulares se consideran convexos. Sin embargo, también existen una infinidad de polígonos irregulares que cumplen con esta característica. Por otro lado, los polígonos cóncavos son menos comunes y se pueden identificar por la presencia de al menos un ángulo interior mayor a 180 grados.
En resumen, la distinción entre polígonos cóncavos y convexos se basa en la medida de los ángulos interiores. Mientras que los polígonos convexos tienen todos sus ángulos menores a 180 grados, los polígonos cóncavos presentan al menos un ángulo que supera esta medida. Esta diferencia es fundamental en la geometría y permite clasificar de forma precisa a los distintos tipos de polígonos.
Dominando las curvas: Una guía completa
¡Descubre cómo dominar las curvas con nuestra guía completa! Aprende técnicas y consejos para mejorar tu técnica de conducción en carreteras sinuosas y saca el máximo provecho de cada curva. Desde la correcta posición del cuerpo hasta la velocidad adecuada, te enseñaremos todo lo que necesitas saber para convertirte en un experto en el arte de dominar las curvas.
Con nuestra guía, te convertirás en un conductor seguro y confiado al enfrentarte a cualquier tipo de curva. No importa si eres un principiante o un conductor experimentado, siempre hay algo nuevo por aprender. ¡Prepárate para disfrutar al máximo de la emoción de conducir en carreteras llenas de curvas y conviértete en un verdadero maestro de la conducción!
Curvas en acción: Aprende y aplica
Descubre cómo las curvas pueden transformar tus diseños con nuestro curso “Curvas en acción: Aprende y aplica”. Aprenderás a utilizar las curvas de manera efectiva para crear diseños más dinámicos y atractivos. Desde la creación de formas orgánicas hasta la manipulación de líneas y contornos, este curso te proporcionará las herramientas necesarias para llevar tus diseños al siguiente nivel. ¡Inscríbete ahora y comienza a dar vida a tus creaciones con curvas en acción!
En resumen, las curvas concavas y convexas son elementos fundamentales en el análisis geométrico y matemático, permitiendo visualizar de manera clara y precisa la dirección de la función en un determinado intervalo. Su estudio es crucial para comprender el comportamiento de las funciones en diferentes contextos, facilitando la toma de decisiones en diversos campos de la ciencia y la ingeniería. Dominar estos conceptos es esencial para avanzar en el estudio de las matemáticas y aplicarlos de manera efectiva en la resolución de problemas.