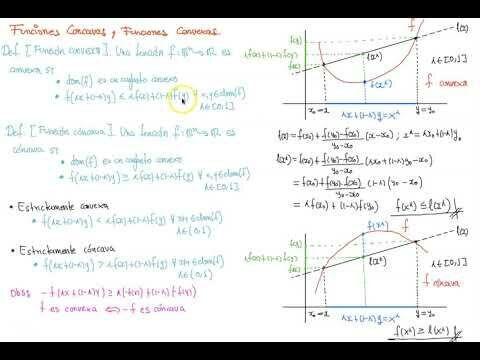
Las funciones cóncavas y convexas son conceptos fundamentales en el estudio del cálculo y el análisis matemático. Estas funciones, que describen la curvatura de una gráfica, tienen aplicaciones en diversas áreas como la economía, la física y la ingeniería. Comprender la naturaleza y las propiedades de las funciones cóncavas y convexas es esencial para resolver problemas de optimización y modelar fenómenos naturales. En este artículo exploraremos en detalle estas funciones y su importancia en el mundo de las matemáticas.
¿Qué es una función cóncava y convexa?
Una función cóncava es aquella que tiene la forma de una curva que se abre hacia arriba, como un arco. Por otro lado, una función convexa es aquella que tiene la forma de una curva que se abre hacia abajo, como un cuenco. En una función convexa, cualquier punto en el fondo de la curva es un mínimo extremo, mientras que en una función cóncava, cualquier punto en el ápice de la curva es un máximo extremo.
En resumen, una función cóncava es aquella que tiene su punto más alto en el ápice de la curva, lo que la hace cóncava hacia abajo, mientras que una función convexa tiene su punto más bajo en el fondo de la curva, lo que la hace cóncava hacia arriba. En ambos casos, estos puntos extremos son importantes para determinar la concavidad o convexidad de la función.
¿Cuál es la diferencia entre cóncavo y convexo?
La diferencia entre cóncavo y convexo radica en la percepción visual que tiene la persona observante. Un objeto se considera cóncavo cuando parece tener una profundidad hacia adentro, como un cuenco con cereales o frutos secos que se ven desde arriba. En cambio, un objeto es convexo cuando su forma aparenta sobresalir hacia afuera, en dirección al observador.
¿Cuál es la diferencia entre cóncavo y convexo?
Los polígonos convexos son aquellos en los que todos sus ángulos interiores miden menos de 180 grados, lo que los hace tener una forma más cerrada y compacta. Por otro lado, los polígonos cóncavos son aquellos en los que al menos uno de sus ángulos interiores mide más de 180 grados, lo que les da una forma más abierta y curva. Mientras que los polígonos convexos son comunes en la naturaleza y en la arquitectura, los polígonos cóncavos son menos comunes pero igual de importantes en el estudio de las formas geométricas.
En resumen, la principal diferencia entre polígonos cóncavos y convexos radica en la medida de sus ángulos interiores. Mientras que los polígonos convexos tienen ángulos interiores que miden menos de 180 grados, los polígonos cóncavos tienen al menos un ángulo interior que mide más de 180 grados, lo que les otorga una forma curva y abierta. Ambos tipos de polígonos son relevantes en el estudio de la geometría y tienen aplicaciones en diversos campos.
Explorando las funciones cóncavas y convexas
En el mundo de las matemáticas, las funciones cóncavas y convexas son de suma importancia. Las funciones cóncavas presentan un aspecto curvo hacia abajo, mientras que las funciones convexas muestran una curvatura hacia arriba. Estas funciones tienen propiedades únicas que pueden ser exploradas y aplicadas en diversos contextos, desde la economía hasta la física.
Al estudiar las funciones cóncavas y convexas, es posible identificar puntos críticos donde la concavidad cambia de dirección. Estos puntos son fundamentales para comprender el comportamiento de la función y pueden ayudar a predecir tendencias futuras. Además, las funciones cóncavas y convexas son útiles para optimizar problemas de maximización y minimización, lo que las convierte en herramientas poderosas en el análisis matemático.
Explorar las funciones cóncavas y convexas es un desafío apasionante que nos permite adentrarnos en el fascinante mundo de las matemáticas. Al comprender sus propiedades y aplicaciones, podemos ampliar nuestro conocimiento y mejorar nuestras habilidades analíticas. ¡No dudes en sumergirte en este emocionante viaje matemático y descubrir todo lo que las funciones cóncavas y convexas tienen para ofrecer!
Dominando el arte de las funciones convexas y cóncavas
Si estás buscando comprender a fondo el mundo de las funciones convexas y cóncavas, has llegado al lugar indicado. Dominar estas dos formas de funciones es esencial para entender el comportamiento de muchas estructuras matemáticas y económicas. Las funciones convexas, cuya gráfica se curva hacia arriba, y las funciones cóncavas, cuya gráfica se curva hacia abajo, son fundamentales en cálculo, optimización y teoría de la decisión. Con nuestra guía detallada y ejemplos prácticos, estarás en el camino para dominar el arte de las funciones convexas y cóncavas en poco tiempo.
Nuestra misión es simplificar la comprensión de las funciones convexas y cóncavas, ofreciendo explicaciones claras y ejemplos ilustrativos que te ayudarán a consolidar tus conocimientos. Aprender a identificar, graficar y utilizar estas funciones te abrirá las puertas a un mundo de aplicaciones en disciplinas como la economía, la ingeniería y la física. Con nuestra guía paso a paso, te convertirás en un experto en el arte de las funciones convexas y cóncavas, adquiriendo las habilidades necesarias para abordar problemas complejos con confianza y precisión.
Todo lo que necesitas saber sobre funciones cóncavas y convexas
Las funciones cóncavas y convexas son conceptos fundamentales en el estudio del cálculo y el análisis matemático. Una función es cóncava si su gráfica está situada por debajo de todas sus tangentes, mientras que es convexa si su gráfica está por encima de todas las tangentes. Estas propiedades son de gran importancia en la optimización de funciones, ya que nos permiten identificar puntos críticos y determinar si son máximos o mínimos.
Es crucial comprender la naturaleza de las funciones cóncavas y convexas para realizar análisis detallados de fenómenos físicos, económicos y sociales. Además, su estudio es esencial en la resolución de problemas de optimización en diversas áreas, como la ingeniería, la economía y la física. Conocer las características y el comportamiento de estas funciones nos permite tomar decisiones informadas y resolver problemas de manera eficiente.
Aprende a identificar y graficar funciones cóncavas y convexas
Aprender a identificar funciones cóncavas y convexas es fundamental para comprender el comportamiento de las curvas en un plano cartesiano. Las funciones cóncavas presentan un tramo de crecimiento positivo y acelerado, mientras que las funciones convexas muestran un tramo de crecimiento positivo pero desacelerado. Es importante reconocer estas características para representar de manera precisa el comportamiento de las funciones en un gráfico.
Al graficar funciones cóncavas y convexas, es esencial prestar atención a la concavidad de la curva en cada tramo. Las funciones cóncavas tendrán un aspecto similar a una “U” invertida, mientras que las funciones convexas se asemejarán a una “U” regular. Identificar estas formas en el gráfico nos permitirá visualizar de manera clara y precisa las características de las funciones, facilitando su análisis y comprensión.
En resumen, las funciones cóncavas y convexas son herramientas fundamentales en el estudio del comportamiento de las funciones matemáticas. Su comprensión y aplicación son esenciales para analizar y resolver una amplia gama de problemas en diversos campos, desde la economía hasta la ingeniería. Al entender las propiedades y características de estas funciones, los estudiantes y profesionales pueden tomar decisiones informadas y realizar análisis precisos en sus respectivas disciplinas. Es crucial seguir explorando y profundizando en el estudio de estas funciones para aprovechar al máximo su potencial en el ámbito académico y profesional.